试求库存补充频度的最优解
分析一下仓储费用的最优化问题
假设我的半年总销量是500件货物,每次找厂家订货大约需要80元订货手续费用(包括电话、出差、合同等),仓库费用0.4元/件/月,假设我的日销售数量是平均的,如果设单次进货量为X的话,总费用包括订货手续费用和仓储费用,总费用的变化趋势是怎样的?X的值多少最合适?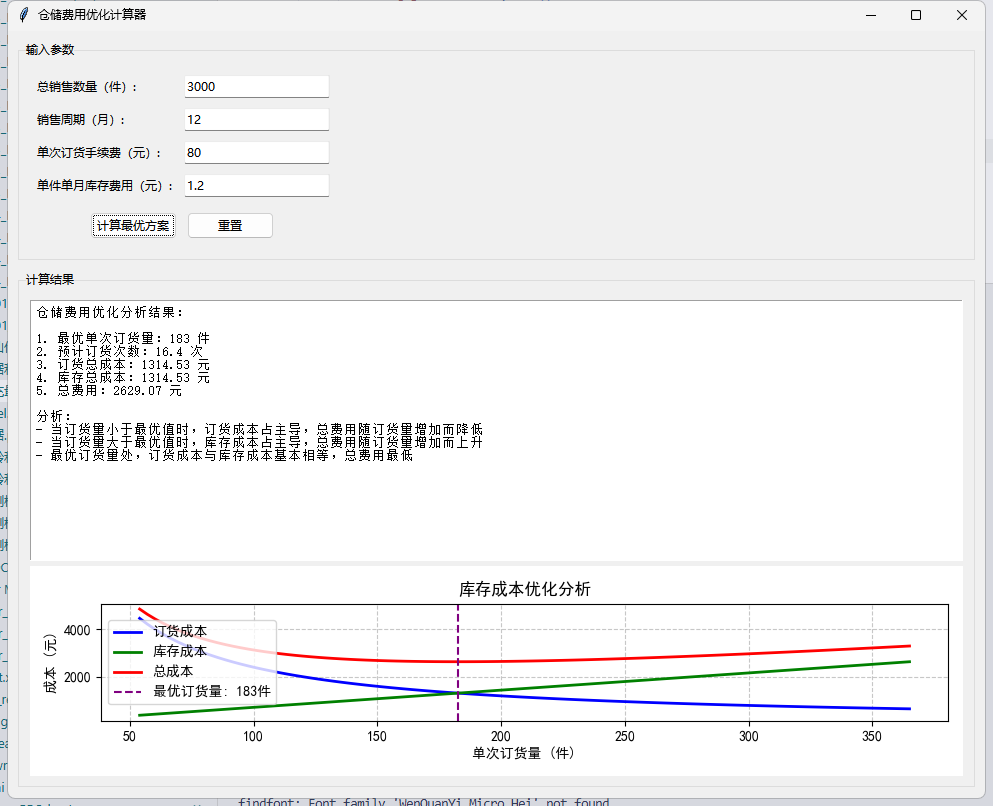
一、先明确核心参数与总费用公式
首先统一时间、成本单位,避免计算偏差:
| 核心参数 | 具体数值与说明 |
|---|---|
| 半年总需求量(D) | 500件(日销量平均,即半年内均匀消耗,日销量=500÷180≈2.78件/天,无需精确到日,按半年维度计算即可) |
| 单次订货成本(S) | 80元/次(固定成本,与进货量X无关,包括手续、差旅等) |
| 单位仓储成本(H) | 0.4元/件/月 → 半年仓储成本=0.4×6=2.4元/件(仓储成本与库存持有时间、数量正相关,需换算为半年单位) |
| 单次进货量(决策变量X) | 每次向厂家订X件,半年内订货次数=总需求量÷进货量=D/X=500/X次 |
总费用(TC)的构成公式
总费用=订货成本+仓储成本,两者此消彼长,需找到平衡点:
- 订货成本:半年内订货次数×单次订货成本 = (D/X)×S = (500/X)×80 = 40000/X
(逻辑:进货量X越小,订货次数越多,订货成本越高;反之则越低) - 仓储成本:平均库存量×单位半年仓储成本 = (X/2)×H = (X/2)×2.4 = 1.2X
(关键逻辑:货物均匀消耗——进货时库存为X,逐渐卖到0,再订下一批,因此平均库存始终是X/2,而非X;仓储成本与平均库存正相关,X越大,平均库存越高,仓储成本越高)
最终总费用公式:
TC = 40000/X + 1.2X
基于此得出以下脚本
import tkinter as tk
from tkinter import ttk, messagebox
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
import math
from matplotlib.figure import Figure
class InventoryOptimizer:
def __init__(self, root):
# 设置中文字体支持
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
self.root = root
self.root.title("仓储费用优化计算器")
self.root.geometry("900x700")
self.root.resizable(True, True)
# 创建主框架
main_frame = ttk.Frame(root, padding="10")
main_frame.pack(fill=tk.BOTH, expand=True)
# 创建输入框架
input_frame = ttk.LabelFrame(main_frame, text="输入参数", padding="10")
input_frame.pack(fill=tk.X, pady=(0, 10))
# 输入字段配置
input_fields = [
("总销售数量(件):", "total_quantity", "500"),
("销售周期(月):", "sales_months", "6"),
("单次订货手续费(元):", "order_cost", "80"),
("单件单月库存费用(元):", "storage_cost", "0.4")
]
# 存储输入变量
self.vars = {}
# 创建输入控件
for i, (label_text, var_name, default) in enumerate(input_fields):
ttk.Label(input_frame, text=label_text).grid(
row=i, column=0, padx=5, pady=5, sticky=tk.W
)
self.vars[var_name] = tk.StringVar(value=default)
ttk.Entry(input_frame, textvariable=self.vars[var_name], width=20).grid(
row=i, column=1, padx=5, pady=5, sticky=tk.W
)
# 计算按钮
btn_frame = ttk.Frame(input_frame)
btn_frame.grid(row=len(input_fields), column=0, columnspan=2, pady=10)
ttk.Button(btn_frame, text="计算最优方案", command=self.calculate).pack(side=tk.LEFT, padx=5)
ttk.Button(btn_frame, text="重置", command=self.reset).pack(side=tk.LEFT, padx=5)
# 创建结果框架
result_frame = ttk.LabelFrame(main_frame, text="计算结果", padding="10")
result_frame.pack(fill=tk.BOTH, expand=True)
# 结果面板
result_paned = ttk.PanedWindow(result_frame, orient=tk.VERTICAL)
result_paned.pack(fill=tk.BOTH, expand=True)
# 文本结果区域
text_frame = ttk.Frame(result_paned, height=150)
result_paned.add(text_frame, weight=1)
self.result_text = tk.Text(text_frame, wrap=tk.WORD, padx=5, pady=5)
self.result_text.pack(fill=tk.BOTH, expand=True)
self.result_text.config(state=tk.DISABLED)
# 图表区域
chart_frame = ttk.Frame(result_paned)
result_paned.add(chart_frame, weight=3)
# 创建图表
self.fig = Figure(figsize=(8, 4), dpi=100)
self.ax = self.fig.add_subplot(111)
self.canvas = FigureCanvasTkAgg(self.fig, master=chart_frame)
self.canvas.get_tk_widget().pack(fill=tk.BOTH, expand=True)
def calculate(self):
"""计算最优订货量并显示结果"""
try:
# 获取输入参数
D = float(self.vars["total_quantity"].get()) # 总需求量
T = float(self.vars["sales_months"].get()) # 销售月数
S = float(self.vars["order_cost"].get()) # 单次订货成本
H_monthly = float(self.vars["storage_cost"].get()) # 单件单月库存成本
H = H_monthly * T # 单件总周期库存成本
# 计算最优订货量 (EOQ模型)
eoq = math.sqrt((2 * D * S) / H)
optimal_order_quantity = round(eoq)
# 计算相关成本
order_count = D / eoq # 订货次数
optimal_order_cost = order_count * S # 最优订货成本
optimal_storage_cost = (eoq / 2) * H # 最优库存成本
total_cost = optimal_order_cost + optimal_storage_cost # 总成本
# 生成图表数据
x_min = max(1, int(eoq * 0.3)) # 避免x值过小
x_max = int(eoq * 2)
x_values = np.linspace(x_min, x_max, 100) # 生成X值范围
# 计算不同订货量下的成本
order_costs = (D / x_values) * S # 订货成本
storage_costs = (x_values / 2) * H # 库存成本
total_costs = order_costs + storage_costs # 总成本
# 清空之前的图表
self.ax.clear()
# 绘制成本曲线
self.ax.plot(x_values, order_costs, label='订货成本', color='blue', linewidth=2)
self.ax.plot(x_values, storage_costs, label='库存成本', color='green', linewidth=2)
self.ax.plot(x_values, total_costs, label='总成本', color='red', linewidth=2)
# 标记最优订货量
self.ax.axvline(x=eoq, color='purple', linestyle='--',
label=f'最优订货量: {optimal_order_quantity}件')
# 图表设置
self.ax.set_xlabel('单次订货量 (件)')
self.ax.set_ylabel('成本 (元)')
self.ax.set_title('库存成本优化分析')
self.ax.legend()
self.ax.grid(True, linestyle='--', alpha=0.7)
self.fig.tight_layout()
# 更新画布
self.canvas.draw()
# 显示文本结果
self.result_text.config(state=tk.NORMAL)
self.result_text.delete(1.0, tk.END)
result = "仓储费用优化分析结果:\n\n"
result += f"1. 最优单次订货量:{optimal_order_quantity} 件\n"
result += f"2. 预计订货次数:{order_count:.1f} 次\n"
result += f"3. 订货总成本:{optimal_order_cost:.2f} 元\n"
result += f"4. 库存总成本:{optimal_storage_cost:.2f} 元\n"
result += f"5. 总费用:{total_cost:.2f} 元\n\n"
result += "分析:\n"
result += "- 当订货量小于最优值时,订货成本占主导,总费用随订货量增加而降低\n"
result += "- 当订货量大于最优值时,库存成本占主导,总费用随订货量增加而上升\n"
result += "- 最优订货量处,订货成本与库存成本基本相等,总费用最低"
self.result_text.insert(tk.END, result)
self.result_text.config(state=tk.DISABLED)
except ValueError:
messagebox.showerror("输入错误", "请确保所有输入都是有效的数字")
except Exception as e:
messagebox.showerror("计算错误", f"计算过程中出现错误: {str(e)}")
def reset(self):
"""重置输入和结果"""
for var in self.vars.values():
var.set("")
self.result_text.config(state=tk.NORMAL)
self.result_text.delete(1.0, tk.END)
self.result_text.config(state=tk.DISABLED)
self.ax.clear()
self.canvas.draw()
if __name__ == "__main__":
root = tk.Tk()
app = InventoryOptimizer(root)
root.mainloop()